Amit Rotem | Virginia Tech

About Me

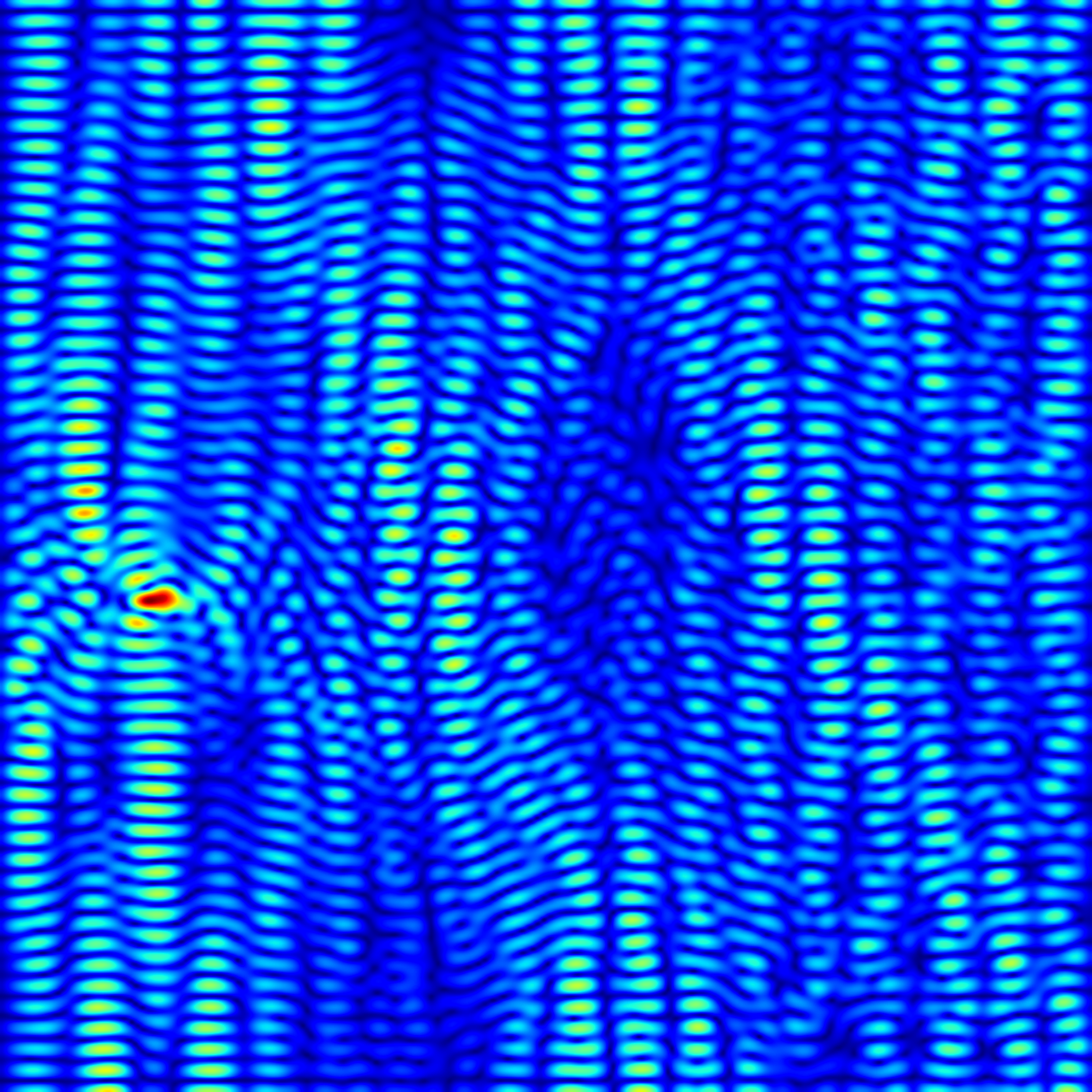
I am a Ph.D. student in the Department of Mathematics at Virginia Tech, advised by Daniel Appelö. My research focuses on numerical methods for partial differential equations (PDEs) with an emphasis on high-performance computing (HPC). My work lies at the intersection of algorithmic theory and scalable implementation. A central focus of my research is the development of the WaveHoltz method for solving frequency-domain wave propagation problems. This includes a general theory establishing convergence in the semi-discrete setting, alongside the design of computational strategies that are efficient on modern parallel architectures. I am actively working on extending the WaveHoltz algorithm to multiscale modeling, and domain decomposition, enabling scalable solvers for increasingly complex physical systems.

I earned both my B.S. and M.S. in Applied Mathematics and Statistics from the Colorado School of Mines. During that time, I worked on a project using machine learning to enhance the value of hyperspectral data in geosciences, bridging lab-based and field data collection techniques. This experience deepened my interest in combining applied mathematics with real-world applications.

I have contributed to the MFEM finite element library, where I implemented a matrix-free interior penalty DG diffusion operator optimized for multi-GPU computing. In addition to my research at Virginia Tech, I collaborate with researchers at Lawrence Livermore National Laboratory on the GenDiL (Generic Discretization Library) project, which focuses on flexible, high-performance implementations of finite element methods in arbitrary dimensions. This collaboration began during a research internship at LLNL.

Outside of research, I enjoy running, hiking, and traveling — not just to conferences 😉. I’m an avid reader of fantasy novels and a fan of horror movies. I value curiosity and creativity both in and out of academic work.

Research Interests

Numerical PDEs: finite element methods, finite difference methods, WaveHoltz, domain decomposition.
High Performance Computing: GPU and many-core distributed algorithms and implementations in C++.

Ongoing Research

WaveHoltz HMM: Combining heterogenous multiscale methods (HMM) for the wave equation with WaveHoltz to solve frequency domain multiscale problems.
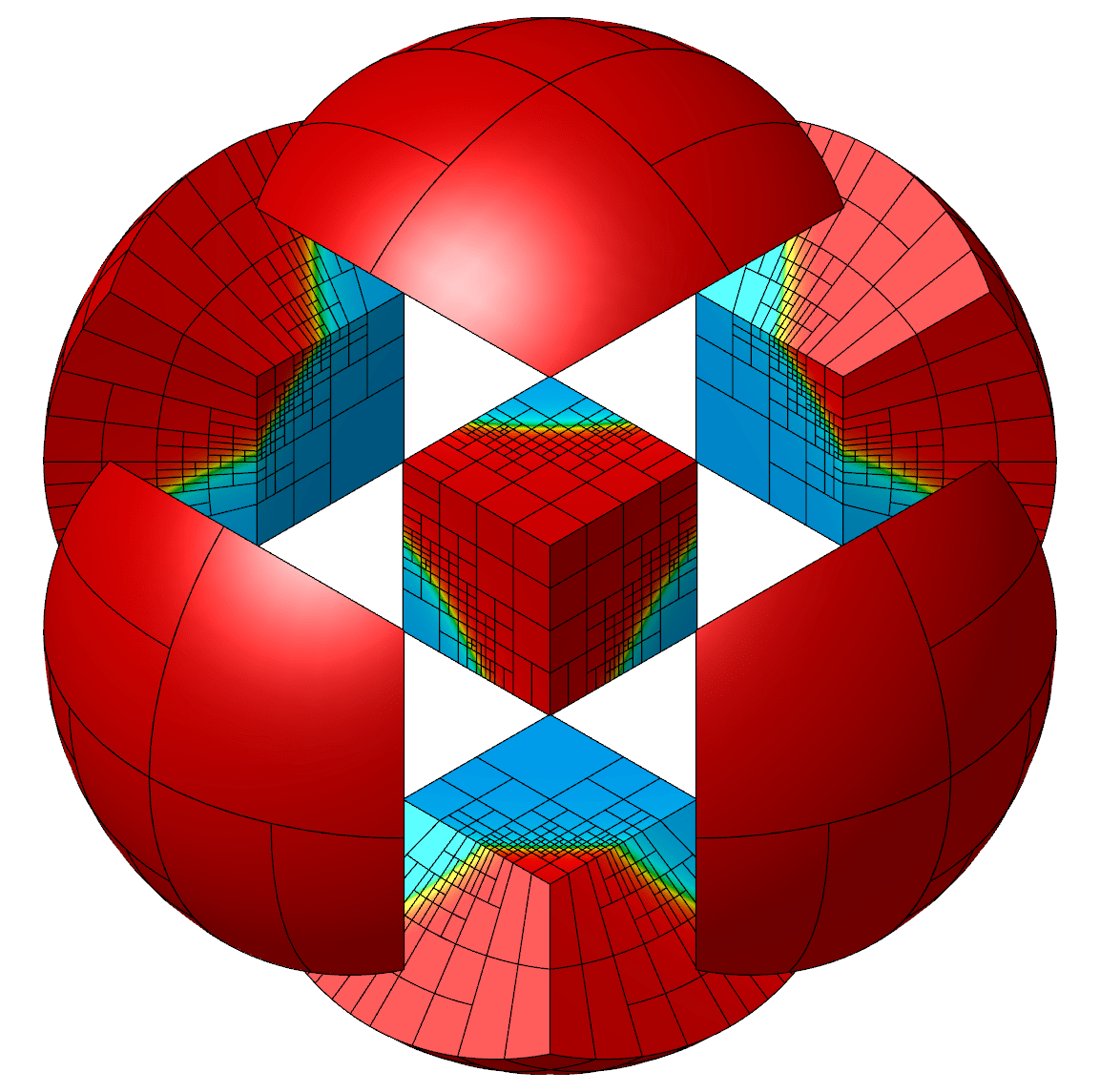
Domain Decomposition on GPUs: Developing scalable algorithm and implementation of the non-overlapping domain decomposition method for the Helmholtz equation which is specialized for massively parallel shared memory hardware (GPUs).
Low Rank Solvers: Developing sub-linear numerical methods for PDEs in low-rank format (SVD and tensor-decompositions).

Publications

Convergence of the Semi-Discrete WaveHoltz Iteration

Amit Rotem, Olof Runborg, Daniel Appelö

PDF FD code DG code preprint

A Domain Decomposition Approach to Accelerate Simulations of Structure Preserving Nematic Liquid Crystal Models

Sylver Carter, Amit Rotem, Shawn W Walker

PDF

Interpretation of Hyperspectral Shortwave Infrared Core Scanning Data Using SEM-Based Automated Mineralogy: a Machine Learning Approach

Amit Rotem, Alexander Vidal, Katharina Pfaff, Luis Tenorio, Matthias Chung, Erik Tharalson, Thomas Monecke

PDF

Research Software Projects

C++, CUDA

CuDDHelmholtz

Domain decomposition solver for the Helmholtz equation implemented in CUDA.

Code 3D solver in progress.

C++, CUDA

GenDiL

GenDiL is a header-only C++ library providing flexible and efficient discretization tools for partial differential equations (PDEs) through a generic programming approach. The library aims to bring advanced mathematical concepts into practical use, leveraging modern C++ for high-performance scientific computing.

Code Maintainer

C++, CUDA

MFEM

MFEM is a modular parallel C++ library for finite element methods. Its goal is to enable high-performance scalable finite element discretization research and application development on a wide variety of platforms, ranging from laptops to supercomputers.

Code Contributor (implemented matrix-free SIPDG Diffusion operator)

C++, MPI

WaveDG

Discontinuous Galerkin implementation of the acoustic wave equation and other conservation laws.

Code

C++

TensorView

TensorView is a single header template library defining several classes used to structure contiguous arrays into tensor-like objects (like numpy's ndarray) whose rank (aka dimension or order) is known at compile time.

Code

C++

Numerics

A collection of numerical methods ranging from nonlinear optimization, to ODE solvers, to neural networks.

Code I wrote this code as a personal project as an undergrad.